Prediciendo Precios de Propiedades
En este post estimo tres modelos de regresión para predecir el precio de venta de una propiedad inmobiliaria usando scikit-learn. Las columnas disponibles incluyen 80 columnas con información sobre la localización de las propiedades, su estructura y estado de conservación, su localización y la fecha y condiciones de la venta.
Dado que la variable objetivo es continua, uso 3 modelos de regresión: regresión lineal sin regularización, regresión Ridge y regresión Lasso.
# Importar módulos
import pandas as pd
import numpy as np
# Leer los datos
casas = pd.read_csv("../../public/data/precios_casas/train.csv")
# Primeras filas
print(casas.head())## Id MSSubClass MSZoning ... SaleType SaleCondition SalePrice
## 0 1 60 RL ... WD Normal 208500
## 1 2 20 RL ... WD Normal 181500
## 2 3 60 RL ... WD Normal 223500
## 3 4 70 RL ... WD Abnorml 140000
## 4 5 60 RL ... WD Normal 250000
##
## [5 rows x 81 columns]Cantidad de filas y columnas:
print(casas.shape)## (1460, 81)Datos faltantes
Los datos faltantes son un problema habitual en este tipo de tarea. El primer paso para analizarlo es cuantificar cuantos casos tienen datos faltantes en cada columna:
print(casas.isnull().any().sum())## 19continuas = ["LotArea", "GrLivArea", "GarageArea",
"WoodDeckSF", "OpenPorchSF", "EnclosedPorch",
"3SsnPorch", "ScreenPorch",
"LowQualFinSF", "LotFrontage",
"1stFlrSF", "2ndFlrSF"]Análisis Exploratorio
Variable objetivo: SalePrice
La variable a predecir es el precio de venta de la propiedad. Es continua y no tiene missings. La propiedad promedio se vendió en $ 180.920, la más barata salió $ 34.900 y la más cara $755.000.
casas[["SalePrice"]].describe()## SalePrice
## count 1460.000000
## mean 180921.195890
## std 79442.502883
## min 34900.000000
## 25% 129975.000000
## 50% 163000.000000
## 75% 214000.000000
## max 755000.000000Tiene distribución asimétrica, con la cola larga a la derecha (es más probable que una casa sea más cara que más barata que el promedio). Esta asimetría hace que sea conveniente normalizarla para modelarla.
Defino una función helper_curtosis para anotar los gráficos de asimetría:
def helper_curtosis(x):
# Texto sobre la curtosis de x
# para agregar al gráfico
sk = skew(x)
sk_pval = skewtest(x)[0]
return f'Curtosis:\n{sk:.2f} ({sk_pval:.3f})'import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
from scipy.stats import skew, skewtest
fig, ax = plt.subplots(1, 2, figsize=(12,4))
# SalePrice sin transformar
x = casas["SalePrice"]
sns.distplot(x, kde=False, fit=stats.norm, ax=ax[0])
ax[0].text(400000, 0.000005, helper_curtosis(x), fontsize = 14)
#ax[0].set_title("SalePrice")
# SalePrice transformada
log1_x = np.log1p(casas["SalePrice"])
sns.distplot(log1_x, kde=False, fit=stats.norm, ax=ax[1])
ax[1].text(12.6, 0.6, helper_curtosis(log1_x), fontsize = 14)
ax[1].set_xlabel("log(1+SalePrice)")
_ = fig.suptitle("La transformación x = log(1+x) corrige la asimetría en SalePrice", fontsize=16)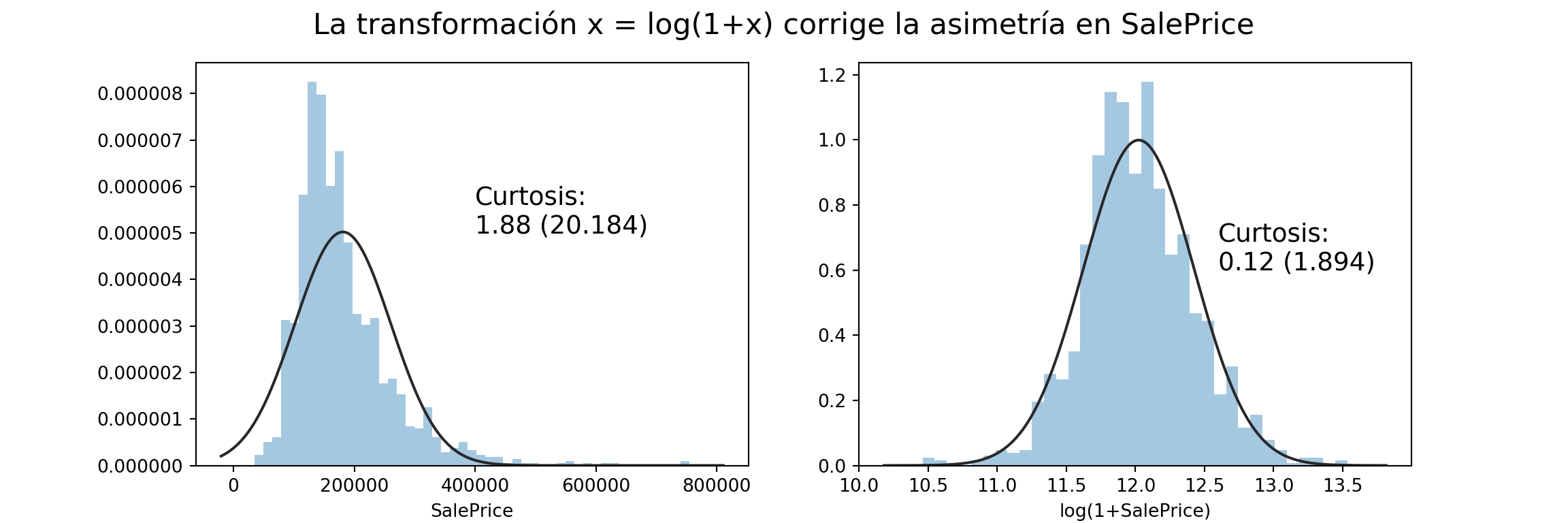
El test de curtosis es una prueba estadística para determinar si la distibución es simétrica. En la variable original rechazamos que la distribución sea simétrica y en la transformada con log(1+x) no rechazamos la hipótesis nula de que la distribución es simétrica.
# Correlaciones con SalePrice
corr_sales_price = casas.corr()["SalePrice"]
# Solo las mayores que 0.63 ordenadas descendiendo
corrs_altas = corr_sales_price[corr_sales_price > 0.4].sort_values(ascending = False)
print(corrs_altas)## SalePrice 1.000000
## OverallQual 0.790982
## GrLivArea 0.708624
## GarageCars 0.640409
## GarageArea 0.623431
## TotalBsmtSF 0.613581
## 1stFlrSF 0.605852
## FullBath 0.560664
## TotRmsAbvGrd 0.533723
## YearBuilt 0.522897
## YearRemodAdd 0.507101
## GarageYrBlt 0.486362
## MasVnrArea 0.477493
## Fireplaces 0.466929
## Name: SalePrice, dtype: float64Calculamos las correlaciones de la variables objetivo con el resto de las variables para determinar en qué variables enfocarnos:
La calidad de la casa (OverallQual), el metraje (GrLivArea), la cantidad de autos que entran en el garage (GarageCars) y el metraje del garage (GarageArea) son las variables continuas más importantes.
Outliers
Hay dos propiedades que tienen valores atípicos.
# Marcar outlier
casas["outlier"] = np.logical_and(casas["GrLivArea"] > 4000,
casas["SalePrice"] < 300000)
# Scatterplot
fig, ax = plt.subplots(1, 2, figsize=(12,4))
_ = sns.scatterplot(x="GrLivArea", y="SalePrice", hue="outlier", data=casas, ax = ax[0])
_ = plt.title("Dos propiedades baratas para su tamaño", fontsize = 16)
_ = ax[1].set(xscale="log", yscale="log")
_ = ax[1].set_xlabel("log") #, ylabel = "log")
_ = sns.scatterplot(x="GrLivArea", y="SalePrice", hue="outlier", data=casas, ax = ax[1])
_ = plt.title("Transformación logarítmica", fontsize = 16)
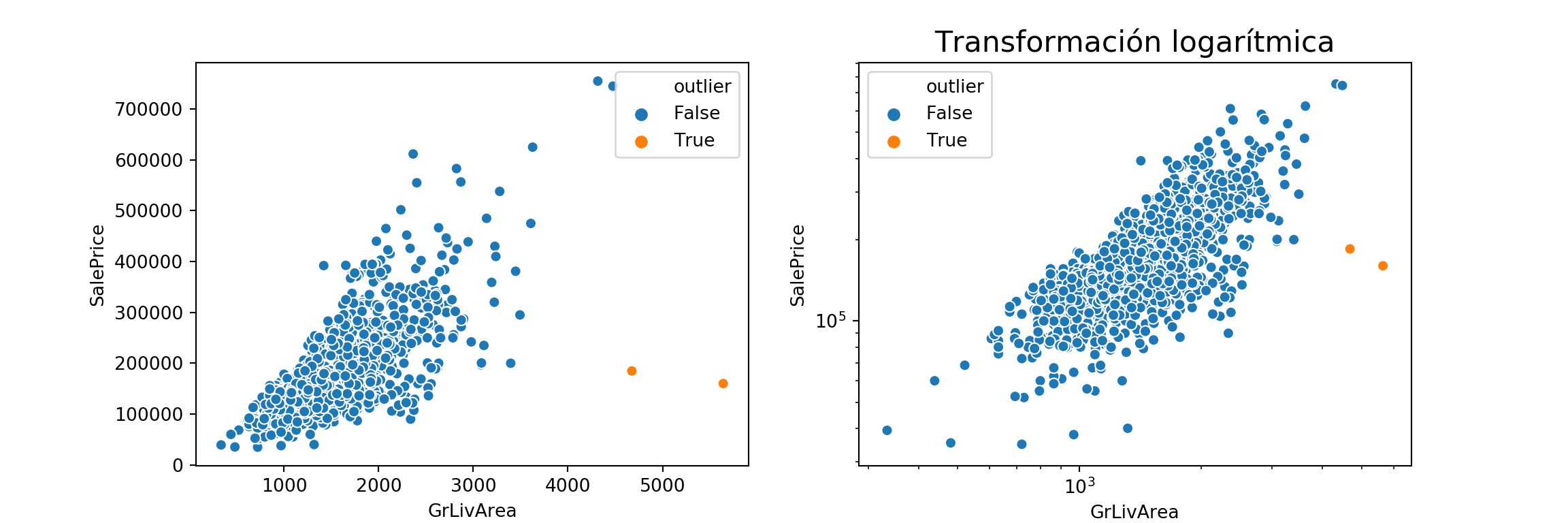
Variables numéricas discontinuas
Estas variables son numéricas pero representan cuentas (cantidad de baños, cantidad de cuartos, etc.).
# Cantidad de baños, cantidad de garages
cuentas = ["KitchenAbvGr", "BedroomAbvGr",
"Fireplaces", "BsmtFullBath",
"TotRmsAbvGrd", "FullBath",
"HalfBath", "YearBuilt"]
# Panel de (2, 3)
dim_panel = (2, 4)
fig, ax = plt.subplots(dim_panel[0], dim_panel[1], figsize=(12,8))
ax[1,3].tick_params(labelbottom = False)
fig.subplots_adjust(hspace=0.4, wspace=0.4)
# Ordenar los nombres de las columnas (2, 3) para iterar fácil
cols = np.reshape(np.array(cuentas)[:8], dim_panel) # tomo los primeros 6 para que entre en el panel
_ = [sns.countplot(x=cols[i, j], data=casas, ax = ax[i, j]) for i in range(dim_panel[0])
for j in range(dim_panel[1])]
plt.show()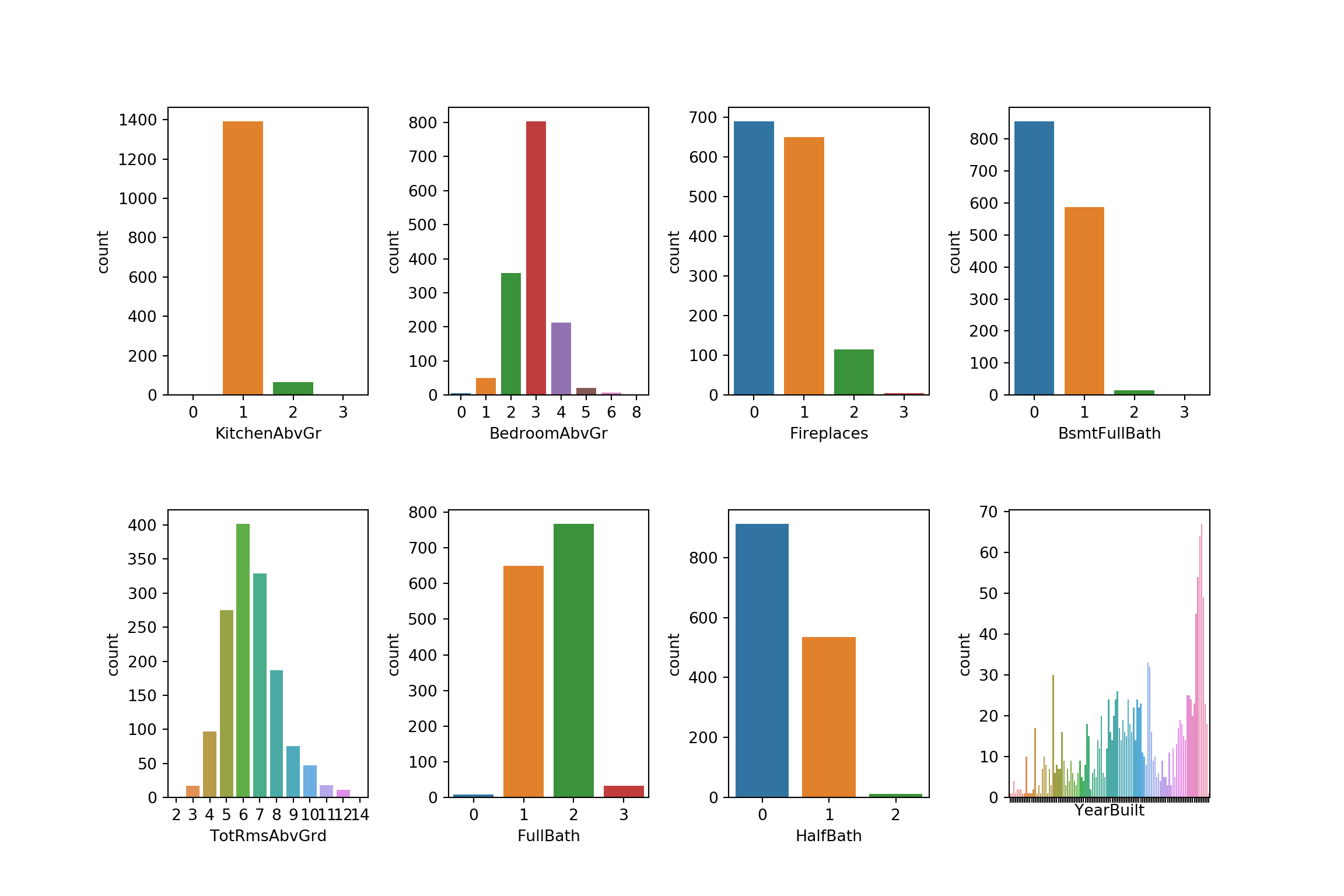
Variables categóricas
Estas variables son categorías y las modelamos como dummies.
categoricas = ["LotShape", "LandContour", "BldgType", "Foundation",
"Neighborhood", "Exterior1st", "LandSlope", "HouseStyle",
"PavedDrive", "SaleCondition", "RoofStyle", "CentralAir",
"LotShape", "LandContour", "MSZoning", "SaleType",
"Street", "Utilities", "Heating", "RoofMatl",
"Exterior2nd", "LotConfig",
"Alley", "Electrical", "BsmtFinType1", "BsmtFinType2", # Tienen Nan
"GarageType", "MiscFeature", "MasVnrType", "Fence" # Tienen Nan
]
dim_panel = (5, 5)
fig, ax = plt.subplots(dim_panel[0], dim_panel[1], figsize=(12,16))
# Apagar los tick labels cuando son demasiados
apagar_ejes = [
(0, 2), (0, 3), (0, 4),
(1, 0), (1, 2), (1, 4),
(2, 0), (2, 2), (2, 3),
(3, 0), (3, 3), (3, 4),
(4, 0), (4, 1), (4, 3), (4, 4)
]
_ = [ax[plt].tick_params(labelbottom = False) for plt in apagar_ejes]
# Fijar los espacios entre los subplots
fig.subplots_adjust(hspace=0.4, wspace=0.6)
cols = np.reshape(np.array(categoricas)[:25], dim_panel)
_ = [sns.countplot(x=cols[i, j], data=casas, ax = ax[i, j]) for i in range(dim_panel[0])
for j in range(dim_panel[1])]
plt.show()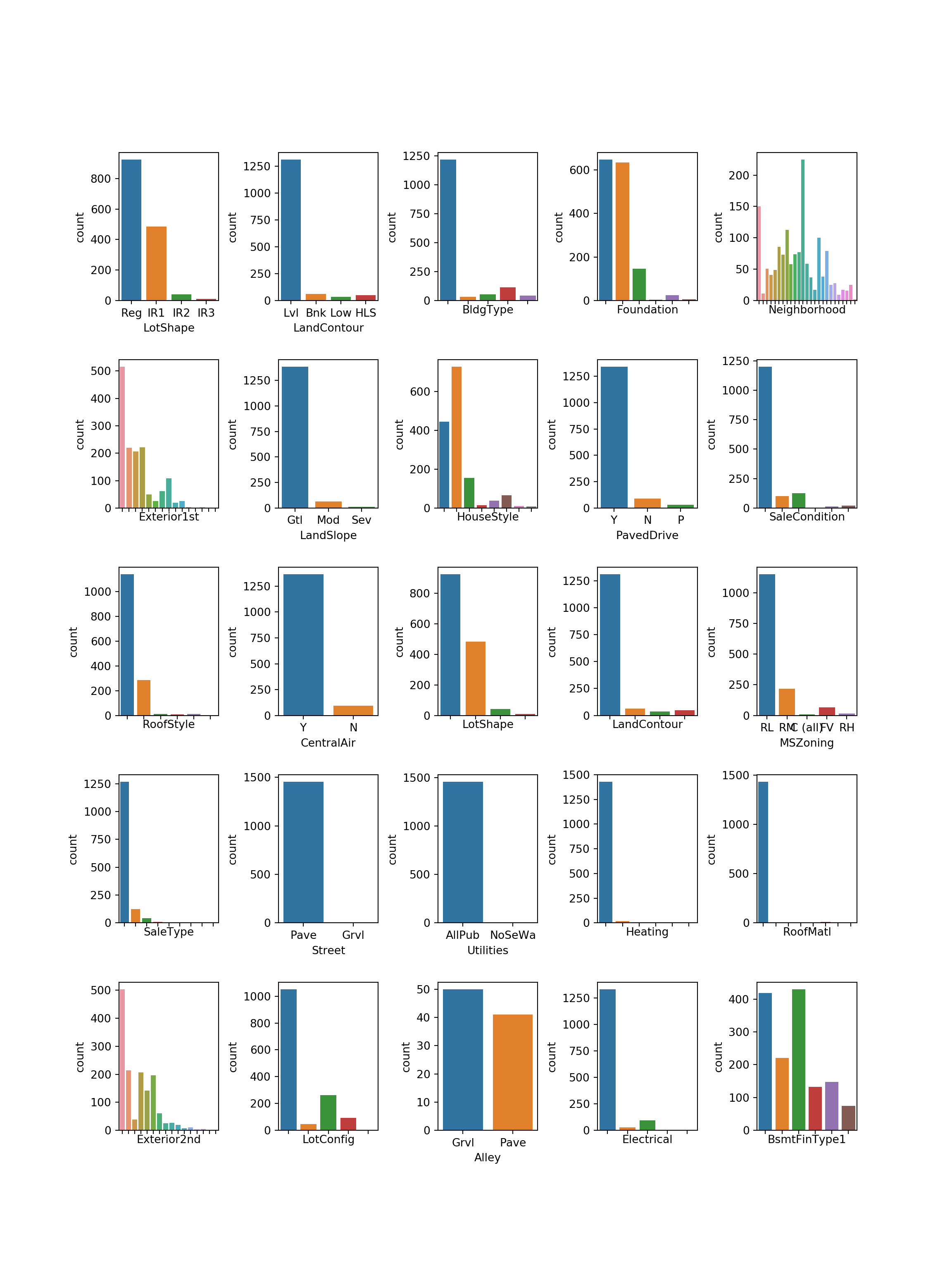
Street, Utilities, Heating y RoofMatl tienen muy poca variación y pueden generar problemas en el modelo.
# Sacar las problematicas
cat_problemas = ["Street", "Utilities", "Heating", "RoofMatl"]
#_ = [ categoricas.remove(col) for col in cat_problemas ]
cat_missing = ["MasVnrType", "GarageType",
#"Electrical", "MiscFeature",
"BsmtFinType1", "BsmtFinType2",
"LotConfig", "Exterior2nd", "LandSlope",
"Alley", "Fence" ]
_ = [ categoricas.remove(col) for col in cat_missing ]Variables Categóricas Ordinales
El último tipo de columna son las variables categóricas ordinales (ej: calidad de la piscina). En estos casos, la variable aparece como texto, pero en realidad queremos modelarla como numérica, porque Calidad = 2 es más que Calidad = 1. Para eso tenemos que recodificar las columnas.
ordinales = ["OverallQual", "OverallCond", "ExterQual",
"ExterCond", "BsmtQual", "BsmtCond",
"BsmtExposure", "HeatingQC", "KitchenQual",
"Functional", "FireplaceQu", "PoolQC",
"GarageFinish", "GarageCond", "GarageQual",
"Fence"] Llevamos las que tienen escalas de calidad (Ex, Gd, Fa, Po) a una escala común. Por ejemplo,cuando es missing la dejamos en 0. Si la calidad de la piscina es missing, es porque la propiedad no tiene piscina y está bien que quede en 0.
def cambiar_escala(df, col, escala):
# reemplazar missings
casas[col].fillna("MISSING", inplace = True)
# aplicar escala_ordinal
casas[col].replace(escala, inplace = True)# Po < Fa < TA < Gd < Ex
ESCALA_ORDINAL = { "MISSING": 0, "Po" : 1, "Fa" : 2,
"TA" : 3, "Gd" : 4, "Ex" : 5}
ordinales_escala_comun = [ "ExterQual", "ExterCond",
"BsmtQual", "BsmtCond",
"HeatingQC", "KitchenQual",
"FireplaceQu", "PoolQC",
"GarageCond" ]
# cambiar casas inplace
_ = [ cambiar_escala(casas, col, ESCALA_ORDINAL) for col in ordinales_escala_comun]ESCALA_FUNCTIONAL = { "Sal" : 0, "Sev" : 1,
"Maj2": 2, "Maj1": 3,
"Mod" : 4, "Min2": 5,
"Min1": 6, "Typ": 7
}
cambiar_escala(casas, "Functional", escala = ESCALA_FUNCTIONAL)# Panel con las variables ordinales
# TODO refactorear a una funcion con las de las cuentas
dim_panel = (4, 4)
fig, ax = plt.subplots(dim_panel[0], dim_panel[1], figsize=(16,18))
# Fijar los espacios entre los subplots
fig.subplots_adjust(hspace=0.3, wspace=0.6)
cols = np.reshape(np.array(ordinales), dim_panel)
_ = [sns.countplot(x=cols[i, j], data=casas, ax = ax[i, j]) for i in range(dim_panel[0])
for j in range(dim_panel[1])]
plt.show()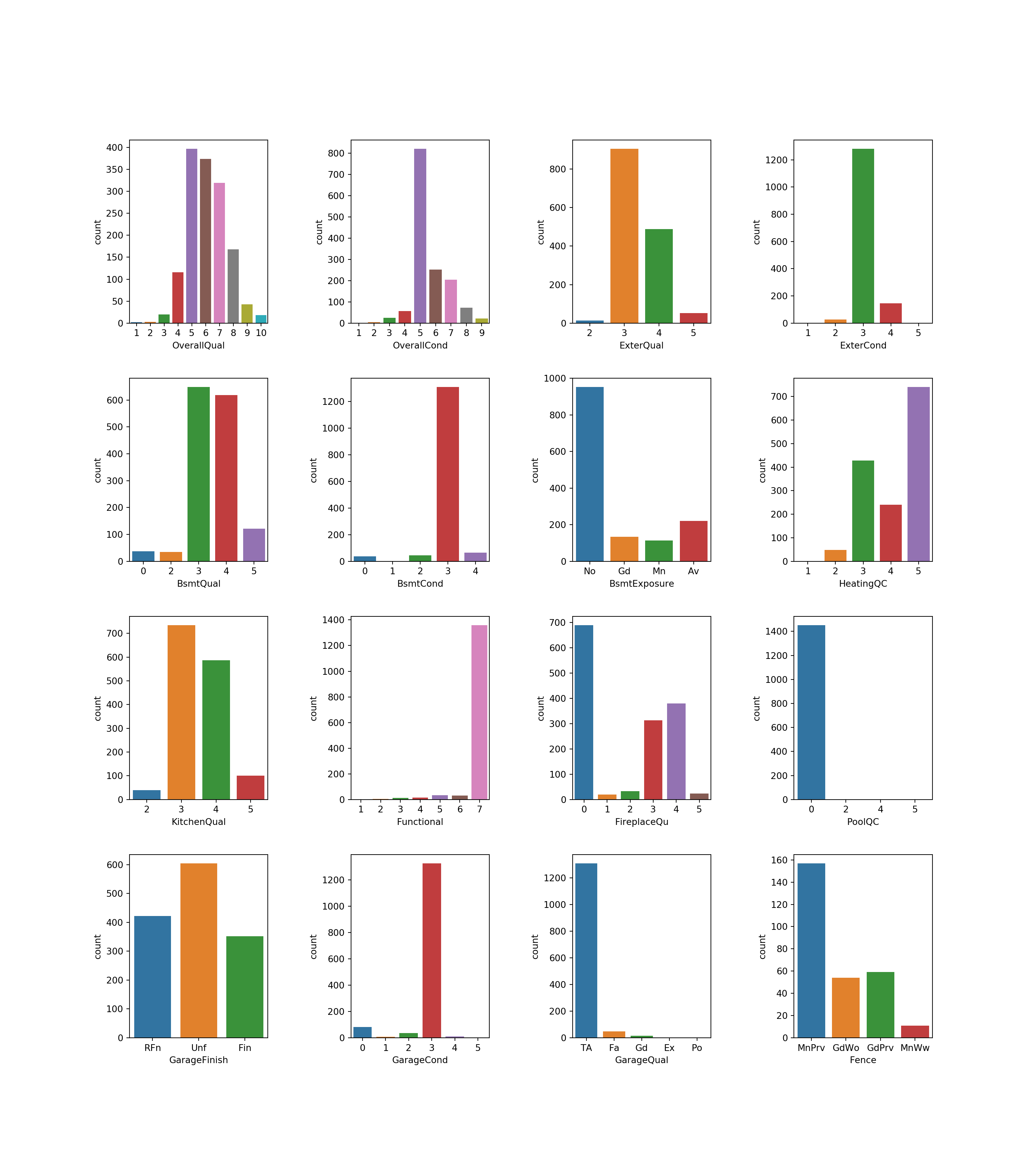
Posibles problemas con PoolQC y Functional. BsmtCond y GarageCond.
Missing en PoolQC (1453) , FireplaceQu (690) , GarageCond (81) , GarageQual (81), GarageFinish (81), GarageType(81), BsmtExposure (38) , BsmtFinType1 (37), BsmtCond (37), BsmtQual (37).
ordinales_missing = ["PoolQC", "FireplaceQu", "GarageCond",
"GarageQual",
"BsmtCond",
"BsmtQual"]
ordinales_problemas = [] # Problematicas
ordinales_escala = ["Fence", "BsmtExposure", "GarageFinish", "ExterCond"] # Estos los saco pq no arme la escala
_ = [ ordinales.remove(col) for col in ordinales_escala + ordinales_missing]Para evitar problemas de multicolinealidad nos quedamos sólo con TotalBsmtSF
# Extraer X e y como arrays
y = casas["SalePrice"]
X = casas[ordinales + categoricas + continuas + cuentas ]
columnas_con_missing = X.columns[X.isnull().any()]
print(f'Columnas con missings para imputar: {columnas_con_missing}')## Columnas con missings para imputar: Index(['Electrical', 'MiscFeature', 'LotFrontage'], dtype='object')
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso, RidgeCV, LassoCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.metrics import make_scorer, mean_absolute_error
from sklearn.model_selection import cross_val_score
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder, StandardScaler, OrdinalEncoder, RobustScaler, FunctionTransformer, PolynomialFeatures
transform_categoricas = Pipeline(steps=[
# Imputar faltantes con el valor mas comun y despues hacer dummies
('imp', SimpleImputer(strategy="most_frequent")),
('onehot', OneHotEncoder(handle_unknown="ignore"))
])
transform_continuas = Pipeline(steps = [
('imp_cont', SimpleImputer(strategy='mean')),
('trans', FunctionTransformer(np.log1p, validate=True)),
('scale', StandardScaler())
])
transform_ordinales = Pipeline(steps = [
('ord', OrdinalEncoder())
])
transform_polys = Pipeline(steps = [
('polys', PolynomialFeatures(2))
])
# ColumnTransformer aplica las pipelines en paralelo y concatena las columnas resultantes
preprocesador = ColumnTransformer(
transformers=[
# ('polys', transform_polys, ["GrLivArea"]),
('cat', transform_categoricas, categoricas),
('num', transform_continuas, continuas + cuentas),
('ord', transform_ordinales, ordinales)
# ('cnts', 'passthrough', cuentas )
]
)Modelos
Estimamos tres modelos: regresión lineal estándar, regresión Ridge y regresión Lasso. La diferencia entre los tres modelos es la forma de regularizar los coeficientes. En el caso de la regresión estándar, se minimiza la suma de cuadrados de los residuos: \(\sum (y - \hat{y})^2\). Ridge y Lasso penalizan la norma del vector de coeficientes \(\theta\). Esto evita el ovefitting a los datos que usamos para entrenar el modelo.
En el caso de la regresión Ridge, se agrega un término a la función de costos un término que incluye la norma \(L_2\) del vector de coeficientes estimados. La regresión Lasso penaliza la norma \(L_1\). Ambos métodos incluyen un parámetro \(\alpha\) que pondera el costo de la norma del vector de coeficientes en la función de costos del modelo. Para determinar el valor de este parámetro, uso Cross-Validation con 5 folds.
Hay dos métricas posibles para evaluar los modelos de regresión: Mean Absolute y Mean Squared Error. El MSE penaliza más los outliers, pero no está medido en la misma unidad que la variable objetivo, por lo que vamos a usar el MAE, que si se mide en la unidad de la variable de destino (en este caso son dólares)
scorer = make_scorer(mean_absolute_error)
X_prep = preprocesador.fit_transform(X) # TODO: este paso debería estar adentro del
# pipeline pero no funciona Regresión sin Regularización
reg = TransformedTargetRegressor(regressor=LinearRegression(),
func=np.log1p,
inverse_func=np.expm1)
cv_linreg = cross_val_score(reg, X_prep, y, cv = 5, scoring = scorer)
print(f'MAE Sin Reg: ${cv_linreg.mean():.2f}')## MAE Sin Reg: $16604.95Lasso
lassoCV = TransformedTargetRegressor(regressor=LassoCV(cv = 5),
func=np.log1p,
inverse_func=np.expm1)
lassoCV_score = cross_val_score(lassoCV, X_prep, y, cv = 5, scoring = scorer)
print(f'MAE Lasso: ${lassoCV_score.mean():.2f}')## MAE Lasso: $15978.56lassoCV.fit(X_prep, y)## TransformedTargetRegressor(check_inverse=True, func=<ufunc 'log1p'>,
## inverse_func=<ufunc 'expm1'>,
## regressor=LassoCV(alphas=None, copy_X=True, cv=5, eps=0.001, fit_intercept=True,
## max_iter=1000, n_alphas=100, n_jobs=None, normalize=False,
## positive=False, precompute='auto', random_state=None,
## selection='cyclic', tol=0.0001, verbose=False),
## transformer=None)print(f'Mejor Alpha: {lassoCV.regressor_.alpha_:.2f}')
## Mejor Alpha: 0.00Ridge
ridgeCV = TransformedTargetRegressor(regressor=RidgeCV(cv = 5),
func=np.log1p,
inverse_func=np.expm1)
ridgeCV_score = cross_val_score(ridgeCV, X_prep, y, cv = 5, scoring = scorer)
print(f'MAE Ridge: ${ridgeCV_score.mean():.2f}')## MAE Ridge: $16462.99ridgeCV.fit(X_prep, y)## TransformedTargetRegressor(check_inverse=True, func=<ufunc 'log1p'>,
## inverse_func=<ufunc 'expm1'>,
## regressor=RidgeCV(alphas=array([ 0.1, 1. , 10. ]), cv=5, fit_intercept=True,
## gcv_mode=None, normalize=False, scoring=None, store_cv_values=False),
## transformer=None)print(f'Mejor Alpha: {ridgeCV.regressor_.alpha_}')
## Mejor Alpha: 10.0Análisis de los Errores
fig, ax = plt.subplots(1, 3, figsize=(16, 4))
reg.fit(X_prep, y)## TransformedTargetRegressor(check_inverse=True, func=<ufunc 'log1p'>,
## inverse_func=<ufunc 'expm1'>,
## regressor=LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
## normalize=False),
## transformer=None)preds = reg.predict(X_prep)
preds = pd.DataFrame({"preds":preds, "true":y})
preds["residuals"] = preds["true"] - preds["preds"]
_ = preds.plot(x = "preds", y = "residuals", kind = "scatter", ax = ax[0])
_ = ax[0].set_title("Sin Regularización")
preds = lassoCV.predict(X_prep)
preds = pd.DataFrame({"preds":preds, "true":y})
preds["residuals"] = preds["true"] - preds["preds"]
_ = preds.plot(x = "preds", y = "residuals", kind = "scatter", ax = ax[1])
_ = ax[1].set_title("Lasso")
preds = ridgeCV.predict(X_prep)
preds = pd.DataFrame({"preds":preds, "true":y})
preds["residuals"] = preds["true"] - preds["preds"]
_ = preds.plot(x = "preds", y = "residuals", kind = "scatter", ax = ax[2])
_ = ax[2].set_title("Ridge")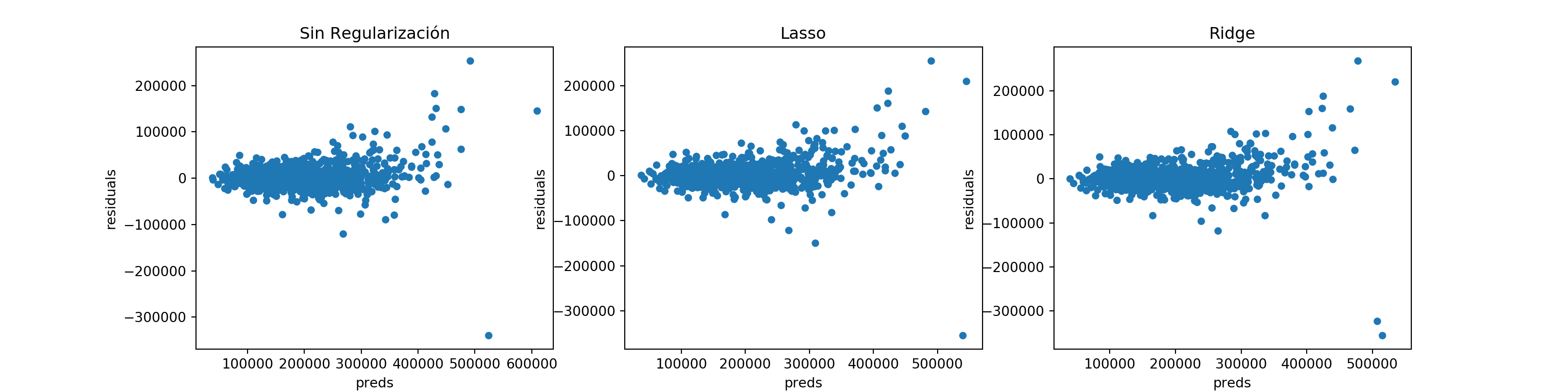
Los errores de los tres modelos muestran que hay margen para mejora porque los errores de predicción son sistemáticamente altos para valores alto de la predicción. Agregar cuadrados de los features podría mejorar los resultados.
Conclusiones
Entrenamos 3 modelos y elegimos los hiperparámetros con un esquema de Cross-Validation con 5 folds. El mejor modelo es la regresión Lasso con \(\alpha = 0.00045\), que permite predecir el precio de una vivienda con un error promedio de aproximadamente $ 15.100, menos del 10% de la media de la variable objetivo ($181.000). Dada la alta cantidad de columnas colineales en los regresores, era de esperar que Lasso funcionara mejor, porque tiende a hace que muchos de los coeficientes \(\theta\) estimados sean 0.